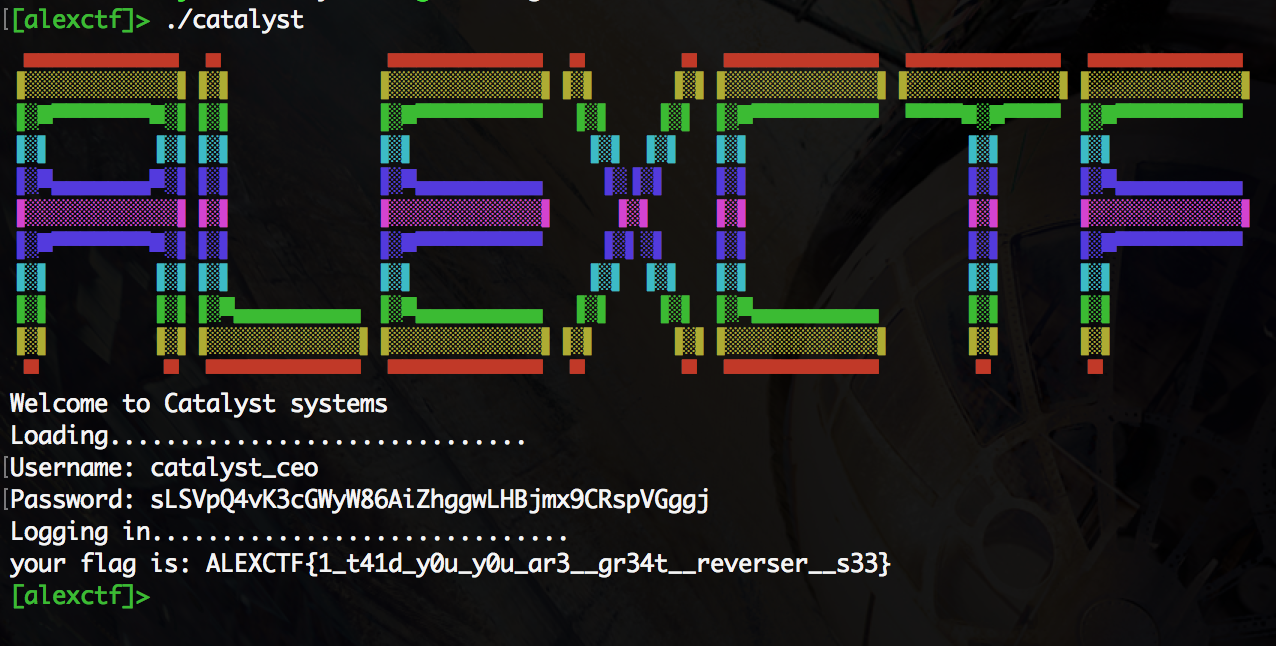
AlexCTF 2017: Catalyst System (150 pts)
Feb 06, 2017AlexCTF just finished this weekend and our team did pretty well, solving all but two of the challenges. In this post I’ll talk about my solution to one of the reverse engineering challenges, called “Catalyst system.” You can check out the raw binary here.
Like most reverse engineering challenges, this binary was a “crackme,” where the challenge is to find a password that causes the binary to give you the flag. When we ran the binary we saw this:
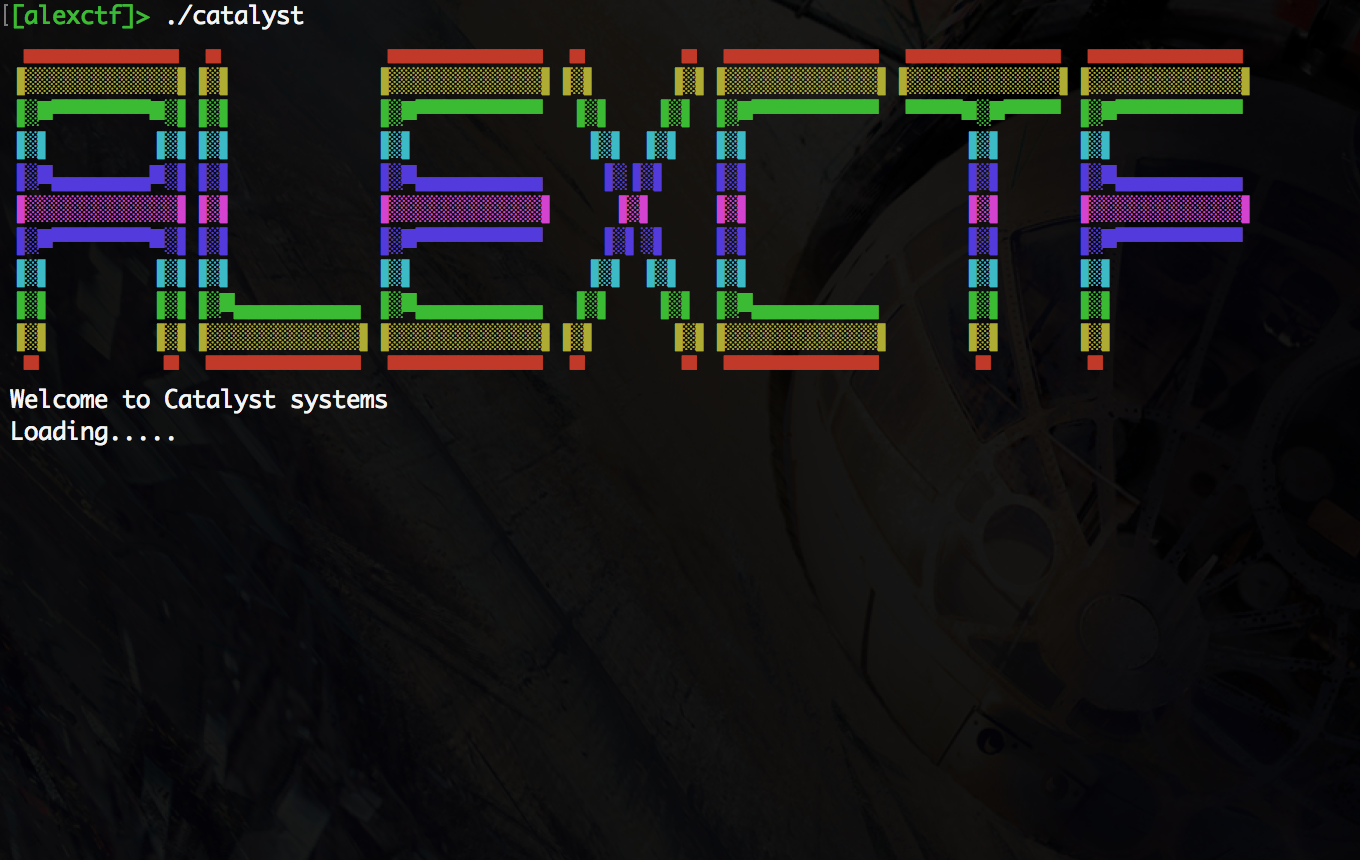
The “Loading” took a while to finish, but once it did it prompted us for a username and password. If you input a wrong pair, it exits immediately.
I did most of my analysis using Hopper, an interactive dissasembler. The first thing I did was open Hopper, select the binary, and look at the “Strings” panel which displays all long runs of valid ASCII characters that it detects in the binary:
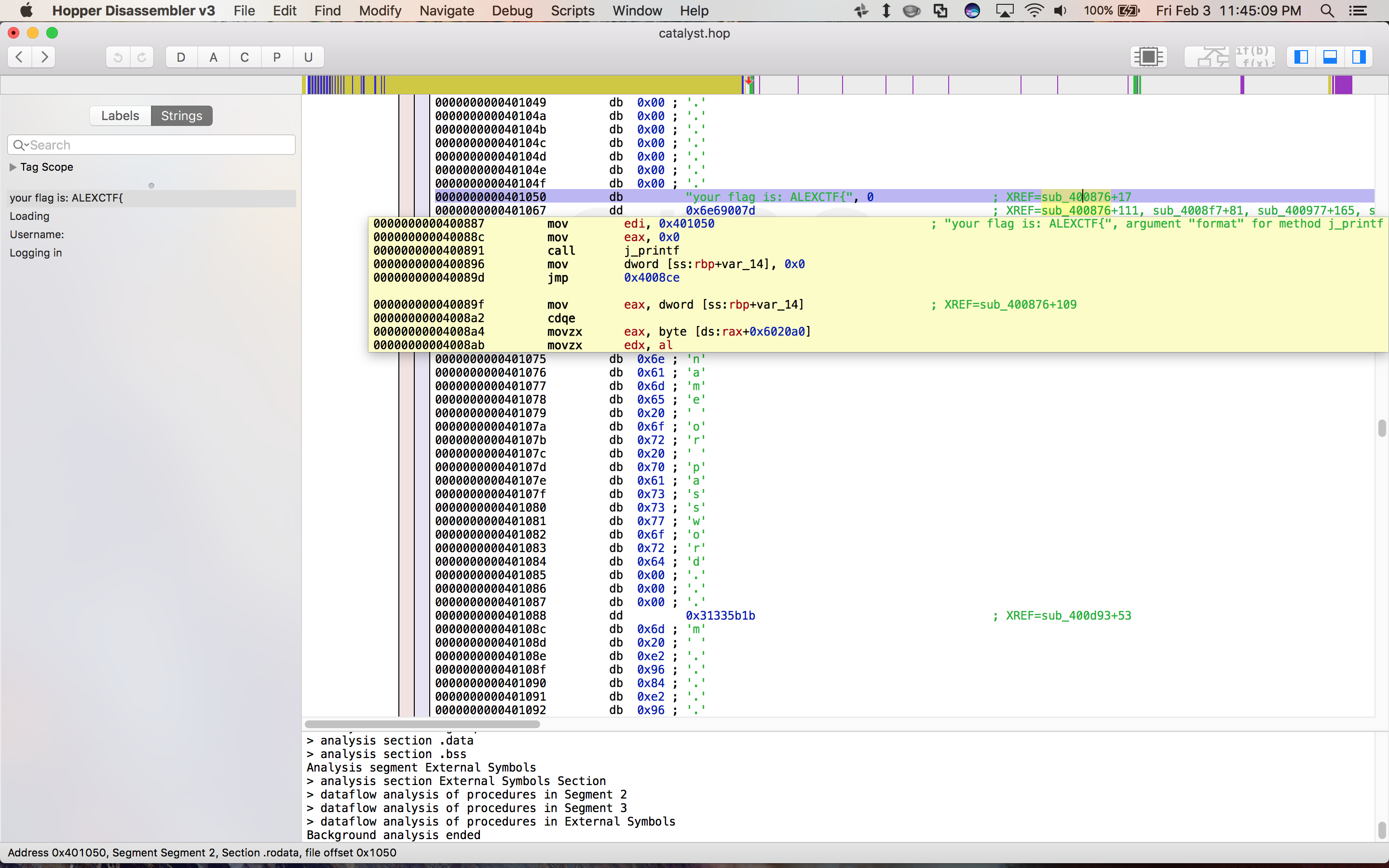
Clearly the string your flag is ALEXCTF{ will be relevant. Hopper shows you where in the assembly the string is referenced and lets you jump to that point:
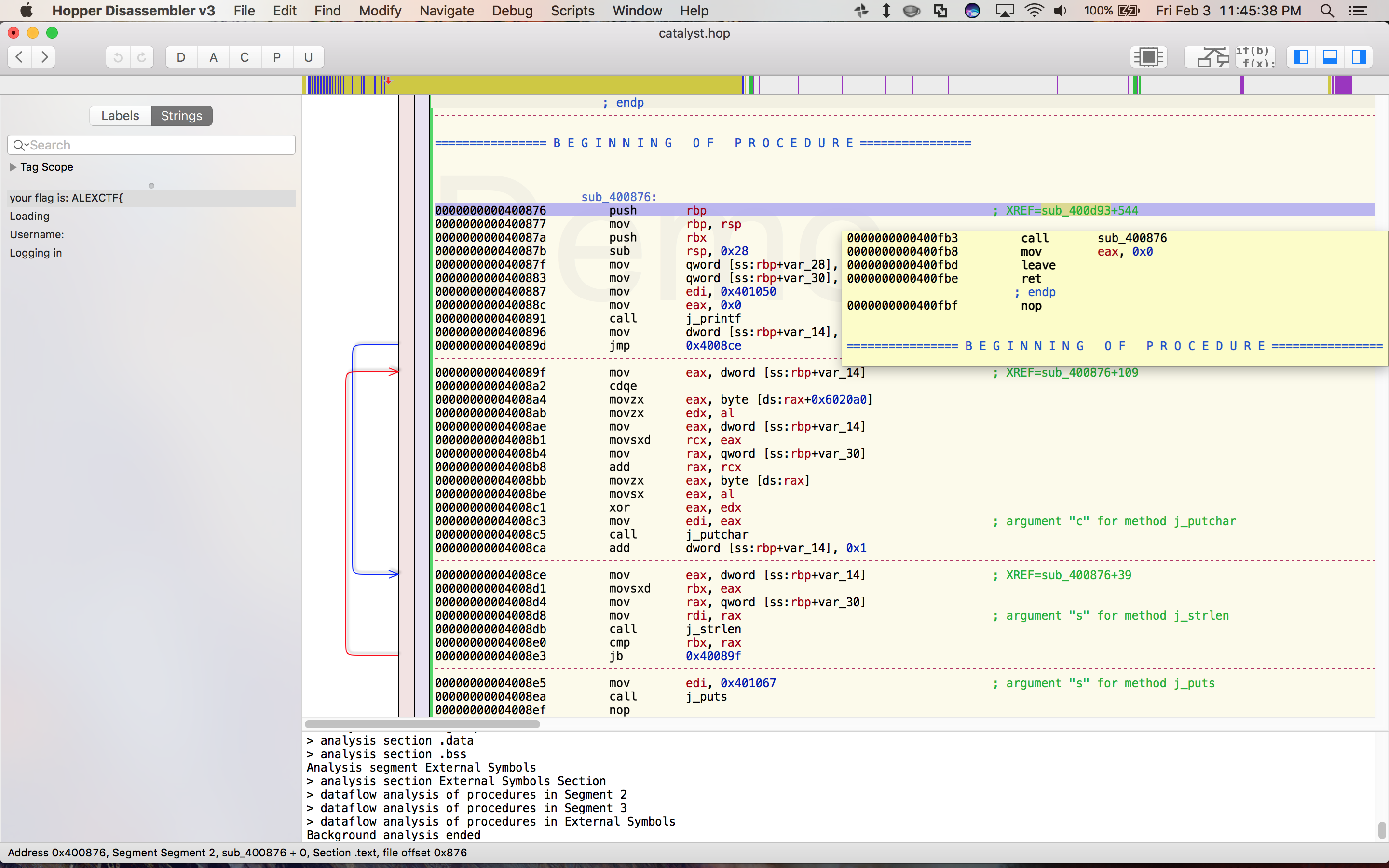
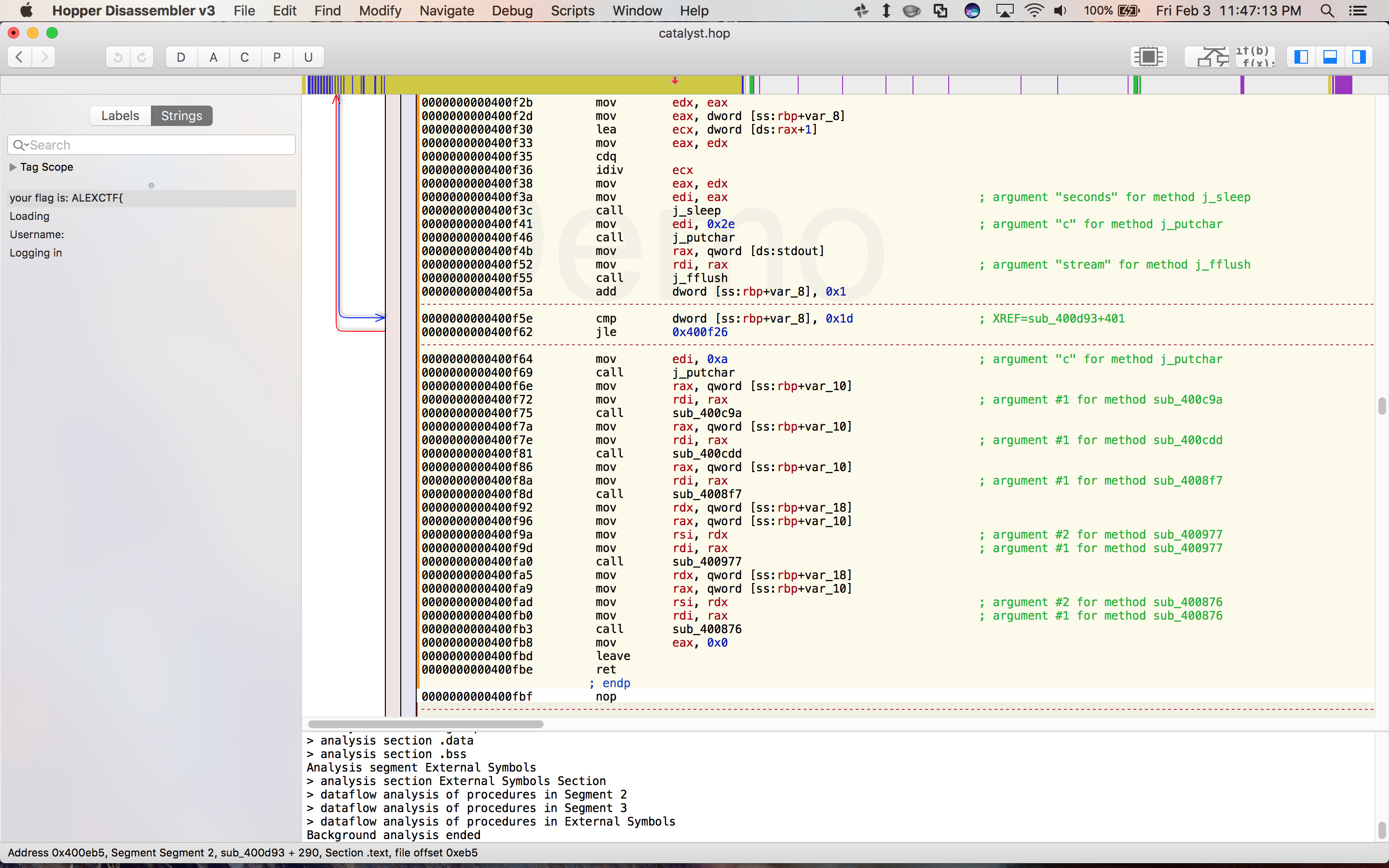
So if we ever get to this subroutine, the binary will just spit out the flag for us. Helpfully, Hopper also tells you which subroutines call this one, and let you jump to them. After jumping around a little bit, you get a pretty good sense of the control flow at work:
- First the binary prints out the colorful logo, and then spends a long time “loading” by repeatedly calling
sleep. - Then, it prompts the user for a username and password.
- Next, it runs a battery of tests against these two strings and exits at the first failure.
- If all the tests pass, it jumps to the subroutine we found earlier and prints out the flag, which is some function of the username and password.
You can see the four tests it runs here:
Our task is to read the four subroutines (sub_400c9a, sub_400cdd, sub_4008f7, and sub_400977) and figure out what they are testing so we can determine a valid username and password.
The first test takes only the username as an argument and immediately computes its length. It then passes this length to another subroutine through the %edi register:
sub_400c41:
0000000000400c41 push rbp
0000000000400c42 mov rbp, rsp
0000000000400c45 sub rsp, 0x20
0000000000400c49 mov dword [ss:rbp+var_14], edi // X = len(username)
0000000000400c4c mov eax, dword [ss:rbp+var_14]
0000000000400c4f sar eax, 0x2
0000000000400c52 mov dword [ss:rbp+var_4], eax
0000000000400c55 mov eax, dword [ss:rbp+var_4]
0000000000400c58 shl eax, 0x2
0000000000400c5b cmp eax, dword [ss:rbp+var_14] // X = 0 (mod 4)
0000000000400c5e jne 0x400c83
0000000000400c60 mov eax, dword [ss:rbp+var_4]
0000000000400c63 sar eax, 0x2
0000000000400c66 mov dword [ss:rbp+var_8], eax
0000000000400c69 mov eax, dword [ss:rbp+var_8]
0000000000400c6c shl eax, 0x2
0000000000400c6f cmp eax, dword [ss:rbp+var_4] // X ≠ 0 (mod 16)
0000000000400c72 je 0x400c83
0000000000400c74 mov eax, dword [ss:rbp+var_4]
0000000000400c77 sar eax, 0x1
0000000000400c79 test eax, eax // X > 8
0000000000400c7b je 0x400c83
0000000000400c7d cmp dword [ss:rbp+var_8], 0x0 // X < 16
0000000000400c81 je 0x400c97
0000000000400c83 mov edi, 0x401069
0000000000400c88 call j_puts
0000000000400c8d mov edi, 0x0
0000000000400c92 call j_exit
0000000000400c97 nop
0000000000400c98 leave
0000000000400c99 ret
; endp
This subroutine is essentially just a series of checks equivalent to the following:
x = len(username)
assert (x >> 2) << 2 == x
y = x >> 2
assert (y >> 2) << y != y
assert (x >> 1) != 0
assert y == 0This code checks that the length is divisible by 4, but not by 16, and that the length is greater than 8 but less than 16. This tells us that the length must be 12.
The second test is a little more interesting:
sub_400cdd:
0000000000400cdd push rbp
0000000000400cde mov rbp, rsp
0000000000400ce1 sub rsp, 0x30
0000000000400ce5 mov qword [ss:rbp+var_28], rdi
0000000000400ce9 mov rax, qword [ss:rbp+var_28]
0000000000400ced mov qword [ss:rbp+var_8], rax
0000000000400cf1 mov rax, qword [ss:rbp+var_8]
0000000000400cf5 mov eax, dword [ds:rax]
0000000000400cf7 mov eax, eax
0000000000400cf9 mov qword [ss:rbp+var_10], rax
0000000000400cfd mov rax, qword [ss:rbp+var_8]
0000000000400d01 add rax, 0x4
0000000000400d05 mov eax, dword [ds:rax]
0000000000400d07 mov eax, eax
0000000000400d09 mov qword [ss:rbp+var_18], rax
0000000000400d0d mov rax, qword [ss:rbp+var_8]
0000000000400d11 add rax, 0x8
0000000000400d15 mov eax, dword [ds:rax]
0000000000400d17 mov eax, eax
0000000000400d19 mov qword [ss:rbp+var_20], rax
0000000000400d1d mov rax, qword [ss:rbp+var_10]
0000000000400d21 sub rax, qword [ss:rbp+var_18]
0000000000400d25 mov rdx, rax
0000000000400d28 mov rax, qword [ss:rbp+var_20]
0000000000400d2c add rax, rdx
0000000000400d2f cmp rax, 0x5c664b56
0000000000400d35 jne 0x400d7c
0000000000400d37 mov rdx, qword `[ss:rbp+var_10]`
0000000000400d3b mov rax, qword [ss:rbp+var_20]
0000000000400d3f add rdx, rax
0000000000400d42 mov rax, rdx
0000000000400d45 add rax, rax
0000000000400d48 add rdx, rax
0000000000400d4b mov rax, qword [ss:rbp+var_18]
0000000000400d4f add rdx, rax
0000000000400d52 movabs rax, 0x2e700c7b2
0000000000400d5c cmp rdx, rax
0000000000400d5f jne 0x400d7c
0000000000400d61 mov rax, qword [ss:rbp+var_18]
0000000000400d65 imul rax, qword [ss:rbp+var_20]
0000000000400d6a mov rdx, rax
0000000000400d6d movabs rax, 0x32ac30689a6ad314
0000000000400d77 cmp rdx, rax
0000000000400d7a je 0x400d90
0000000000400d7c mov edi, 0x401069
0000000000400d81 call j_puts
0000000000400d86 mov edi, 0x0
0000000000400d8b call j_exit
0000000000400d90 nop
0000000000400d91 leave
0000000000400d92 ret
; endp
Essentially it interprets the 12-character username as three 32-bit integers stored in [ss:rbp+var_10], [ss:rbp+var_18], and [ss:rbp+var_10]. Let’s call these values A, B, and C respectively. It then computes a series of functions on these three values and verifies that they equal certain constants. Namely:
A - B + C == 0x5c664b56
B + (A + C) * 3 == 0x2e700c7b2
B * C == 0x32ac30689a6ad314
This gives us three equations and three variables, so we can solve them to get: A = 0x61746163, B = 0x7473796c, and C = 0x6f65635f. Putting them all together (and remembering that integers are interpreted as little-endian), we find that the username is catalyst_ceo:
>>> import struct
>>> ''.join([struct.pack('<I', x) for x in [0x61746163,0x7473796c,0x6f65635f]])
'catalyst_ceo'
The third test simply checks that the username consists of only lowercase characters or underscores. The fourth test takes in both the username and password as arguments. It first checks that the password consists of only alphanumeric characters. Then it does something interesting:
0000000000400a4c mov rax, qword [ss:rbp+var_20]
0000000000400a50 mov edx, dword [ds:rax]
0000000000400a52 mov rax, qword [ss:rbp+var_20]
0000000000400a56 add rax, 0x4
0000000000400a5a mov eax, dword [ds:rax]
0000000000400a5c add edx, eax
0000000000400a5e mov rax, qword [ss:rbp+var_20]
0000000000400a62 add rax, 0x8
0000000000400a66 mov eax, dword [ds:rax]
0000000000400a68 add eax, edx
0000000000400a6a mov edi, eax ; argument "seed" for method j_srand
0000000000400a6c call j_srand
0000000000400a71 mov rax, qword [ss:rbp+var_28]
0000000000400a75 mov ebx, dword [ds:rax]
0000000000400a77 call j_rand
0000000000400a7c sub ebx, eax
0000000000400a7e mov eax, ebx
0000000000400a80 cmp eax, 0x55eb052a
0000000000400a85 je 0x400a9b
0000000000400a87 mov edi, 0x401069
0000000000400a8c call j_puts
0000000000400a91 mov edi, 0x0
0000000000400a96 call j_exit
The username is stored at [ss:rbp+var_20] and the password at [ss:rbp+var_28]. It’s computing A + B + C and then seeding the random number generator with this value. It then calls rand and subtracts the resulting value from the first 32-bits of the password, checking that the result equals 0x55eb052a.
It then does this over and over again for the subsequent characters of the password. If all the comparisons work out, the subroutine returns and will print out our flag.
We can write a simple C program to seed the generator with the correct value and spit out the first few integers it produces:
#include <stdio.h> /* printf, scanf, puts, NULL */
#include <stdlib.h> /* srand, rand */
int main ()
{
unsigned int seed = 0x61746163 + 0x6f65635f + 0x7473796c;
/* initialize random seed: */
srand (seed);
int i;
for(i = 0; i < 10; i++) {
printf("0x%x, ", rand());
}
return 0;
}We then just need to add these to each of the constants and string the results together:
>>> import struct
>>> a = [0x55eb052a, 0xef76c39, 0xcc1e2d64, 0xc7b6c6f5, 0x26941bfa, 0x260cf0f3, 0x10d4caef, 0xc666e824, 0xfc89459c, 0x2413073a]
>>> b = [0x684749, 0x673ce537, 0x7b4505e7, 0x70a0b262, 0x33d5253c, 0x515a7675, 0x596d7d5d, 0x7cd29049, 0x59e72db6, 0x4654600d]
>>> ''.join([struct.pack('<I', (x + y) % (1 << 32)) for (x, y) in zip(a, b)])
'sLSVpQ4vK3cGWyW86AiZhggwLHBjmx9CRspVGggj'
Now we have both our username and password, so we can actually just feed them both to the binary and get the flag. The binary intentionally makes this step annoying: because of all the calls to sleep you have to wait a while before it prints out the flag. We can either patch the binary to remove these calls, or continue with our static analysis.
Let’s do the latter. This is the subroutine that prints out our flag:
sub_400876:
0000000000400876 push rbp
0000000000400877 mov rbp, rsp
000000000040087a push rbx
000000000040087b sub rsp, 0x28
000000000040087f mov qword [ss:rbp+var_28], rdi
0000000000400883 mov qword [ss:rbp+var_30], rsi
0000000000400887 mov edi, 0x401050 ; "your flag is: ALEXCTF{", argument "format" for method j_printf
000000000040088c mov eax, 0x0
0000000000400891 call j_printf
0000000000400896 mov dword [ss:rbp+var_14], 0x0
000000000040089d jmp 0x4008ce
000000000040089f mov eax, dword [ss:rbp+var_14]
00000000004008a2 cdqe
00000000004008a4 movzx eax, byte [ds:rax+0x6020a0]
00000000004008ab movzx edx, al
00000000004008ae mov eax, dword [ss:rbp+var_14]
00000000004008b1 movsxd rcx, eax
00000000004008b4 mov rax, qword [ss:rbp+var_30]
00000000004008b8 add rax, rcx
00000000004008bb movzx eax, byte [ds:rax]
00000000004008be movsx eax, al
00000000004008c1 xor eax, edx
00000000004008c3 mov edi, eax ; argument "c" for method j_putchar
00000000004008c5 call j_putchar
00000000004008ca add dword [ss:rbp+var_14], 0x1
00000000004008ce mov eax, dword [ss:rbp+var_14]
00000000004008d1 movsxd rbx, eax
00000000004008d4 mov rax, qword [ss:rbp+var_30]
00000000004008d8 mov rdi, rax ; argument "s" for method j_strlen
00000000004008db call j_strlen
00000000004008e0 cmp rbx, rax
00000000004008e3 jb 0x40089f
00000000004008e5 mov edi, 0x401067 ; argument "s" for method j_puts
00000000004008ea call j_puts
00000000004008ef nop
00000000004008f0 add rsp, 0x28
00000000004008f4 pop rbx
00000000004008f5 pop rbp
00000000004008f6 ret
; endp
The username is stored at [ss:rbp+var_28] and the password at [ss:rbp+var_30]. This function just iterates over the password string, and xors it character by character against a string stored at [ds:0x6020a0]. We can simulate this pretty fast in python:
>>> s = "42 13 27 62 41 35 6B 0F 7B 46 3C 3E 67 0C 08 59 44 72 36 05 0F 15 54 43 38 17 1D 18 08 0E 5C 31 21 16 02 09 18 14 54 59"
>>> x = [int(a, 16) for a in s.split(' ')]
>>> p = 'sLSVpQ4vK3cGWyW86AiZhggwLHBjmx9CRspVGggj'
>>> ''.join([chr( ord(p[i]) ^ x[i]) for i in range(len(p))])
'1_t41d_y0u_y0u_ar3__gr34t__reverser__s33'
Our flag is ALEXCTF{1_t41d_y0u_y0u_ar3__gr34t__reverser__s33}. This is confirmed by the binary: